This article was originally published in ToolTalk, the quarterly newsletter of PAST (www.pasttools.org). It has been enhanced with new data from time to time as information becomes available.
Hollows and rounds are among the most common of wooden planes – probably the most common outside of bench planes (jacks, smoothers, jointers, etc.). Most put them in the general category of molding planes, although there are those who feel they are a separate category unto themselves. I will avoid this philosophical debate, since the purpose of this article is to discuss a different topic that often comes up in old tools circles: what do the size numbers on these planes really mean?
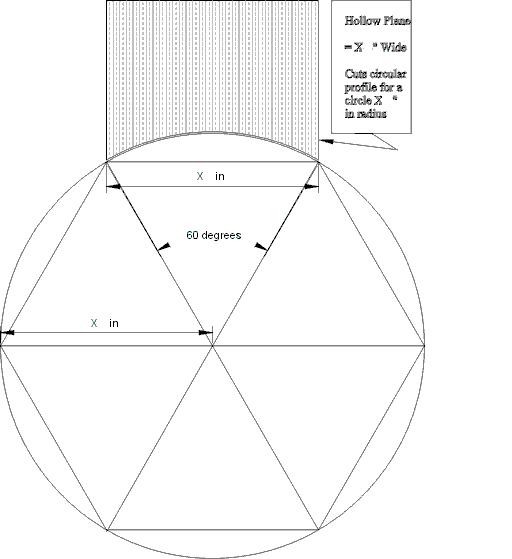
First off, it is useful to understand the relationship between the size of one of these planes and the size of the circle to which it is related. I use this terminology because a hollow (the concave plane) does not actually cut a circle in normal use, but rather the outside arc of a circle. Similarly, the round (the convex plane) cuts an inside arc. Traditional hollows and rounds cut an arc equal to one sixth of a circle. Why was this chosen as a standard?
While plane makers were probably better craftsman than mathematicians, there is a very practical aspect to this choice. Without getting into any geometrical proofs, a good basic understanding of this principle is quite easy to grasp. Suppose you took a circle and divided it up into six equal portions, marking off six points on the circle to indicate where they were. Now, connect each point to its neighbor. You have just inscribed a hexagon in the circle. If you then connected each point to the center of the circle, you have divided the hexagon into six triangles which can be proved to be equilateral. That means that the distance between two neighboring points on the circle is exactly the same as the radius of the circle.

Now think about a plane designed to match the profile of the outside of the circle from one point to the next, as shown above. The width of the plane iron would be the same as the distance between two adjoining points on the circle. So if you wanted to cut a circle of one inch radius (or two inch diameter), you just reached for a plane with an iron width of one inch. What could be simpler? This only works if the arc of the iron is one sixth of a circle, so it is easy to see why this became a standard.
So much for the easy part. Now we need to consider the actual size numbers stamped on the plane itself. These do not, unfortunately, have a very good correspondence with the size of the plane. Each manufacturer numbered their planes from smallest to largest, with numbers chosen to indicate the relative position of a plane within a full set. Planes were frequently sold as pairs or individually, but sometimes were sold as either a full set or half set. A full set included a pair of each size; a half set usually included only the even numbered pairs of planes.
The problem here is that each manufacturer chose his own numbering system, and so plane size numbers do not often match from one manufacturer to the next. Some copied the numbering system of some other manufacturer, and some companies had more than one numbering system. This was sometimes due to two companies merging (e.g., Ohio Tool and Auburn) or just a different way of doing things in a different era.
Further, some companies did not offer half sets (Ohio Tool is a good example), but simply offered planes only in those sizes that corresponded to the members of a half set. Typically, these planes would increase in iron widths by about 1/8 inch from one marked number to the next. I tend to call this "coarse granularity." This is a common trait among Ohio plane makers; Sandusky uses identical sizing in their 1925 catalog. In contrast, most of the New England makers did offer full and half sets (or at least number their planes according to such a scheme), providing "fine granularity." The difference between two consecutive size numbers in such a scheme would then be 1/16 inch. This is true of the smaller size planes but not necessarily the larger ones, as we shall see.
Why should such a regional difference exist? This is pure speculation on my part, but it should be remembered that in the first half of the 19th century, Ohio was still considered part of the Western frontier. The area around Sandusky was not settled until the 1820's when a group of "immigrants" from Connecticut arrived. In the last half of the century - the "golden age" of wooden plane making - Ohio was starting to be what we call it today, the Midwest. But it still was mostly rural and agrarian. Most of the work done in Ohio was probably functional furniture for everyday use. New England had developed into a center for furniture design, and its more established cities were demanding more ornate furniture for the well-to-do. These had more complex design details, and required more exact tools to meet those requirements.
The following table contains data from an Ohio Tools catalog and provides an example of coarse granularity. It is interesting to note that they sold a set that consisted of pairs 1 through 9, but larger sizes had to purchased as pairs of planes and were not included as part of a set. The larger sizes also carried a different model number (73) from the more common smaller sizes (model 72).
| Number | Iron width | Circle Diameter |
| 1 | ¼ | ½ |
| 2 | 3/8 | ¾ |
| 3 | ½ | 1 |
| 4 | 5/8 | 1 ¼ |
| 5 | ¾ | 1 ½ |
| 6 | 7/8 | 1 ¾ |
| 7 | 1 | 2 |
| 8 | 1 1/8 | 2 ¼ |
| 9 | 1 ¼ | 2 ½ |
| 10 | 1 3/8 | 2 ¾ |
| 11 | 1 ½ | 3 |
| 12 | 1 5/8 | 3 ¼ |
| 13 | 1 ¾ | 3 ½ |
| 14 | 1 7/8 | 3 ¾ |
| 15 | 2 | 4 |
One advantage of this scheme is its consistency. Since the progression is linear, if you know you need a plane one quarter inch larger than the one you are using, you just reach for one with a size stamp that is two numbers higher. The disadvantage is that you might be implementing someone else’s design and they call for a radius of 7/16 inch. Then you are out of luck, since there is no such size in this scheme. This certainly came up sometimes, or there would not be sets built around 1/16 inch increments, and those are quite common. In practical use, planes in eighth inch increments meet the needs of most users, including the author. Although I do have some planes in sixteenth-inch sizes, I could probably live with a "half set" of planes, or a set of planes from a maker like Ohio Tool, without difficulty. Of course, I am not trying to build furniture to someone else’s exact design.
Now that we have looked at a relatively simple scheme, it’s time to consider the more complex one. Finer granularity is called for only in the smaller sizes. You could define a plane numbering system simply by taking the Ohio Tools table, doubling the size numbers, and inserting another line in between each one with a size halfway between its neighbors. Because you don’t really need a 1 7/16 inch round, the incremental size between consecutively numbered planes sometimes changes at some point, which I call a crossover point. Beyond this point, the separation is greater than in the smaller size planes. But not all manufacturers used such a scheme.
Here are two examples from the Chapin-Stephens 1914 catalog reprint, and from the reprint of the 1872 Greenfield Tools Company catalog. We can see that there was no "crossover point" in the Chapin-Stephens line, and that each size was exactly 1/8 inch larger in iron width than its predecessor. But for Greenfield, this increment held only to the #20 pair. The #22 and #24 pair were each 1/4 inch larger in iron width than their predecessors.
We can also see the effect of Greenfield offering a smaller sized plane for the same number than Chapin-Stephens. For each size number, the Greenfield plane is 1/8 inch narrower than the same numbered plane from Chapin-Stephens below the crossover point. But the #22 sized plane is the same for both makers since Greenfield changed the size increment and Chapin-Stephens did not. A #24 plane from Greenfield is larger for the same reason.
| Chapin-Stephens | Greenfield | |||
| Number | Iron Width | Circle Diameter | Iron Width | Circle Diameter |
| 2 | 1/4 | 1/2 | 1/8 | 1/4 |
| 4 | 3/8 | 3/4 | 1/4 | 1/2 |
| 6 | 1/2 | 1 | 3/8 | 3/4 |
| 8 | 5/8 | 1 1/4 | 1/2 | 1 |
| 10 | 3/4 | 1 1/2 | 5/8 | 1 1/4 |
| 12 | 7/8 | 1 3/4 | 3/4 | 1 1/2 |
| 14 | 1 | 2 | 7/8 | 1 3/4 |
| 16 | 1 1/8 | 2 1/4 | 1 | 2 |
| 18 | 1 1/4 | 2 1/2 | 1 1/8 | 2 1/4 |
| 20 | 1 3/8 | 2 3/4 | 1 1/4 | 2 1/2 |
| 22 | 1 1/2 | 3 | 1 1/2 | 3 |
| 24 | 1 5/8 | 3 1/4 | 1 3/4 | 3 1/2 |
| 26 | 1 3/4 | 3 1/2 | ||
| 28 | 1 7/8 | 3 3/4 | ||
| 30 | 2 | 4 |
While this table only illustrates these two numbering schemes, other plane makers sometimes followed one or the other approach. Ken Roberts' reprint of the Baldwin Arrowmammett catalog of 1857 indicates that this maker used identical sizing to that of Greenfield. My own collection of H. L James planes indicates that Henry James followed the numbering system used by Chapin-Stephens, although I do not have a complete set. This makes it more difficult to know if it "tracked" for all sizes. A published size table or list is the only way to really know the maker's intent.
There is no indication in the catalog that odd numbered planes were offered by Chapin-Stephens. All sets consist of even numbered planes only. You could buy a set of nine, ten, or 12 pairs (always starting from #2). The three largest size pairs, 26 through 30, were always sold separately, as these are less commonly used. In contrast, the Greenfield catalog states that odd numbered planes were offered, and that they fell halfway between the sizes of the even numbered plane on either side. In fact, it was possible to buy a full set from Greenfield, consisting of pairs #1 through #24, although the size of a #1 plane was not specified. Happily, I recently acquired a Greenfield round in this size - the iron measures a bit less than 3/16 inch. The Arrowmammett catalog is a bit more specific. Their number one plane works a 1/8 inch circle, implying a 1/16 inch iron width. You could buy either half sets (even numbers) or full sets from Arrowmammett, and you could choose to end either set at #18, #20, or #24. Many cabinetmakers would not need the larger sizes, as those are more useful for fairly large-scale architectural work.
The Auburn Tool Company catalog indicates that planes were sold either by the half-set (nine even-numbered pairs from number 2 through number 18) or by the pair. The pairs were offered in all sizes, one through 24. It has been reported that A. W. Howland followed the same numbering scheme as Auburn. It is probably a reasonable assumption that Auburn's predecessor company Casey, Clark, & Co. used the same numbering scheme.
At this point, I would only add that fine granularity does not necessarily imply complexity. The Canadian plane maker V. A. Emond, working in Quebec, offered planes with a very simple numbering scheme where the plane number is the iron width in eighths of an inch. A complete set of V. A. Emond planes ranged from a number 1 (1/8 inch) to a number 16 (two inches). A half set consisting of the even-numbered pairs was also offered, as was a quarter set consisting of the 1/2 inch, one inch, 1 1/2 inch, and two inch.
If you are putting together a set of hollows and rounds, there are advantages to choosing a single manufacturer and building up a set from that one maker. The odds of the numbering system being consistent are far better than a mixed set. If you are a collector, this is probably your goal anyway. As a user, I am mostly interested in building things with old tools, so this is less of a concern for me. I generally go looking for a matched pair of planes in a given iron width, rather than looking for a particular size number that is only meaningful for a given maker.
Another thing to be aware of is that manufacturers did change numbering systems. I have always had a fondness for planes from James Kellogg of Amherst, Mass. However, the lack of consistency is so frustrating that I have all but abandoned buying planes form this maker. It is not unusual to have two planes with identical size stamps but completely different widths. If you have to deal with such a maker, it is best to specify planes by the width of the iron and the size mark, or you are apt to be disappointed. Sometimes there are other clues to help pin down the era of manufacture, such as the maker's stamp changing, the size or font of the numbers and letters used in the stamps, or other details. These can help in achieving consistency, since all planes made during one period probably used the the same numbering system.
It should also be mentioned that some makers took a more rational approach to this problem. For example, the Denison family marked the actual size of the plane in inches, not a number in some system. They did keep a consistent size even as the company changed from father to son. But this is more the exception than the rule.
Thanks to Michael D. Sullivan for providing the figure used in this write-up, and to reviewer Bruce van Sloun.
Information in the second table is from the following sources:
Greenfield Tool Company, 1872 Illustrated Catalogue, reprinted (no copyright date appears) by The Astragal Press, Mendham, New Jersey
The Chapin-Stephens Co. 1914 Catalog, reprint (C) 1991 by The Astragal Press, Mendham, New Jersey
Though not specifically included in the tables, information from the following sources was also used:
Illustrated Supplement to the Catalog of Bench Planes, Moulding Tools, &c., Arrowmamett Works, 1857, reprinted 1976 by Ken Roberts Publishing Company, Fitzwilliam, NH
Quebec Steam Plane Factory, V. A. Emond, 1889 catalog, reprint (C) 1995 MacLachlan Woodworking Museum, Kingston, Ontario, Canada